Internetas pilnas specifinių paveikslėlių, kur „ranka piešia ranką“, „diedas laiko rutulį kur matosi jo atspindys“, „paukščių mozaika tolygiai keičia spalvą (diena ir naktis)“ ir klasikinės mozaikos iš driežiukų ar gekonų. Visa tai M. C. Ešerio kūriniai, kuris juos kūrė pirmoje dvidešimto amžiaus pusėje be jokių kompiuterių. Tiesiog paišė, arba kas dar baisiau, raižė akmenyje ar metale. O ten jau nelabai galima suklysti.
Mane kiek labiau sudomino būtent tos mozaikos iš driežiukų. Dėl to, kad jas gražiai galima išpjaustyti lazeriu ir šiaip, jos man patiko. Tai „kaleidoskopinės“ simetrijos piešiniai- kiekvienas turi vieno ar kito lygio simetriją. Kol kas medienoje aš atlikau tik dvi variacijas, o kompiuteryje jau trys. Tai trijų, keturių ir šešių kampų simetrija, pagal klasikinius grafiko darbūs. Tokios mozaikos dar vadinamos angliškai „tessellation“.
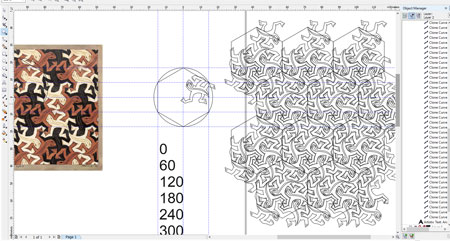
Trikampio simetrija. Pats pirmas bandymas- objektai stovi lygiakraščio trikampio kampuose atitinkamai pasukti 0, 120 ir 270 laipsnių kampų.
Prieš pjaustant tokias mozaikas, jas reikia persipaišyti kokia nors vektorinio paišymo programa. Mano lazeris bendrauja su Corel Draw, todėl ten ir viską paišėm. Ne visi failai kažkaip išliko, bet kas liko tikrai pasidalinsiu straipsnio gale.
Nustačius simetrijos rūšį, kampus ir teisingai paskaičiavus atsikartojimo žingsnį, viskas daroma gana paprastai. Arba taip kaip aš dariau:
Pasirinktą vieną mozaikos elementą pilnai apipaišom viena kreive. Taip pat, vidinius dekoratyvinius elementus įtraukiam į tą pačia, „master“ kreivę. Kreives kiek galima tiksliau privedam prie originalaus „bitmap“ paveikslėlio.
Pasirenkam „master“ kreivę ir darom „clone“ komandą. Gaunam tokią pat kreivę (šiuo atveju driežiuką) kaip ir „master“ kreivėje. Šia klonuotą kreivę dublikuojam (Cntr-D) tiek kartų kiek turime simetrijos variantų (3,4,6 kartus) ir pasukam atitinkamais kampais. Dabar galima dar kiek „pasidublikuoti“ kreivių (neliečiam „master“!) ir surenkam preliminarę mozaiką. Kad ir kaip stengėmės kopijuoti Ešerį, mozaika tiksliai nesusideda. Taip ir turi būti- Ešerio paveikslėliai piešti ranka ir mozaikos elementai nėra visiškai vienodi. Žmogus gi neturėjo kompo. Pastebim pagrindinius simetrijos ir jungties taškus- snukučio priekis, letenėlės pirštelis ar panašiai. Tai bus mūsų atraminiai taškai ir pradedam trinti „master“ kreivėje „nodus“ tol, kol liks toks kiekis, kad mozaikoje driežiukai atrodo pilnai, bet „master“ kreivėje lieka tik draskulos. Tada kreivė mozaikoje gaunasi vienos linijos ir matematiškai tiksli gretutinio driežiuko dalis. Dabar lazeris pjaus tik vieną eilę ir driežiukai bus identiški. Tik svarbu, kad atstumai tarp vienodų driežiukų būtų visame projekte vienodi- priešingu atveju galima kumuliatyvinė klaida ir pats kraštinis driežiukas bus kiek kitoks nei pats pirmas.
Dabar lieka tik technikos problemos- pjovimas, šlifavimas, dažymas, lakavimas, klijavimas ir vėl lakavimas. Nu ir dar rėmelis nepamaišytu.
Kol kas man stačiakampė (keturių driežiukų, nors čia jie panašūs į gekonus) simetrija patinka mažiausiai. Trikampė visai nieko. Deja šešiakampės dar nepamačiau.
Turint vektorinį mozaikos modelį, galima elementus didinti ir išsipjauti žymiai didesnius elementus, kad ir kokį parketą pasigaminti. Reikia tik gauti kokybiškos kietmedžio faneros ir prilaikyti gana daug kantrybės. Tačiau rezultatas jaučiu nenuvils.
Dar bus ir video, o pradžiai keletas Corel failų:Corel Draw failai paišymui.




Oba, kaip fainai 🙂
Pamenu, interneto platybese, esu mates kazkokias grindis ale naciu, ten kazkaip panasiai sisipuzlindavo svastikos. O dar esu mates pavyzdius mediniu grindu, kur su spalvom budavo isgaunami i toli/gyli nubegantys lyg kokie spiraliniai/staciakampiniai portalai. Nu ale atrodydavo, kad tos grindukes is taip sudetu skirtingos spalvos lenteliu isriesdavo vaizda ir gaudavos beveik stereogramos ziurint tam tikru kampu
su arkliai nesigautu ? 🙂
Kastytis Says:
“Pamenu, interneto platybese, esu mates kazkokias grindis ale naciu, ten kazkaip panasiai sisipuzlindavo svastikos…”
http://i.imgur.com/tGUzvEm.png
Nu kazkas panasaus, tik ten buvo marmuras is skirtingu spalvu
Sitai kaip, nenurimau, kol radau:
http://www.bibliotecapleyades.net/sociopolitica/sociopol_thule10.htm
[Edit by admin]